| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 독서 #독서후기 #피로사회 #행동과잉 #긍정과잉
- ESG 채권
- 밑시딥
- MRC
- 안드로이드 구조
- k겹 교차검증
- ESG
- 뉴로 심볼릭
- 다중분류
- 학습 자동 중단
- 면접왕이형
- 면접왕 이형
- 베스트 모델
- 로지스틱 회귀법
- 안드로이드
- 코틀린
- 밑시딥2
- 밑바닥부터 시작하는 딥러닝
- 모두의 딥러닝
- 선형회귀
- nlp
- 예측선
- 보이스피싱
- gradiant descent
- GPT-3
- 경제신문스크랩
- 과적합
- 경사하강법
- 딥페이크
- andoriod with kotlin
- Today
- Total
Practice makes perfect!
[모두의 딥러닝] 6~9장 퍼셉트론, 다층 퍼셉트론, 오차 역전파 본문
퍼셉트론(perceptron) : 신경망을 이루는 가장 중요한 기본 단위
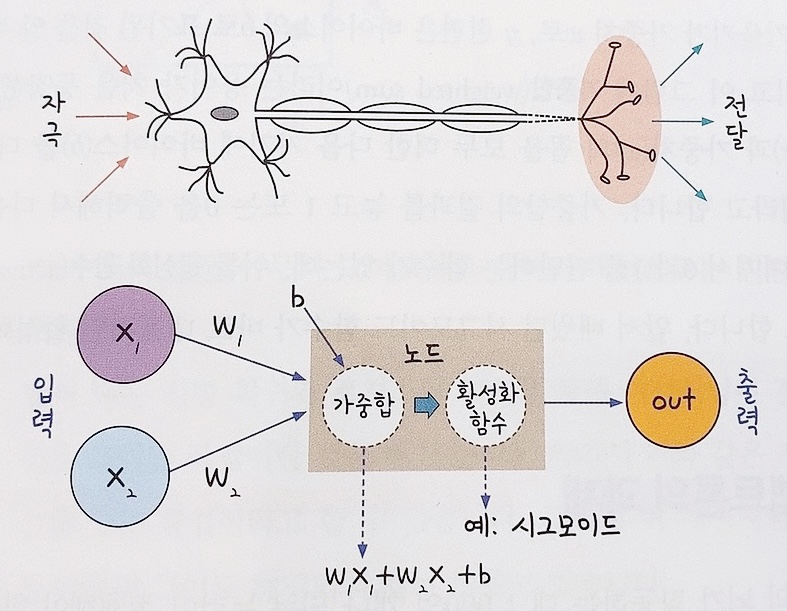
1. 가중치, 가중합, 바이어스, 활성화 함수

가중치 w (weight)
가중합 (weighted sum)
바이어스 (bias)
활성화 함수 (activation function) - ex) 시그모이드 함수
2. XOR 문제
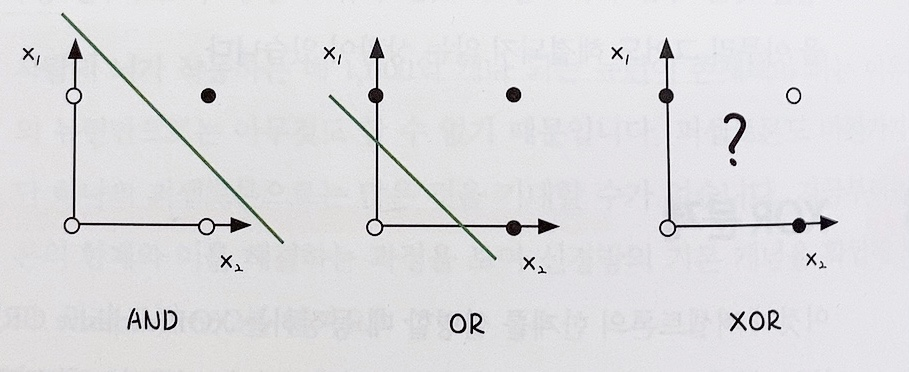
AND와 OR 게이트와 달리 XOR 게이트는 선을 그어 결과값이 1인 값을 구별할 수 없다.
10여 년이 지난 후에야 이 문제를 해결한 개념이 다층 퍼셉트론(multilayer perceptron)이다.
3. 다층 퍼셉트론
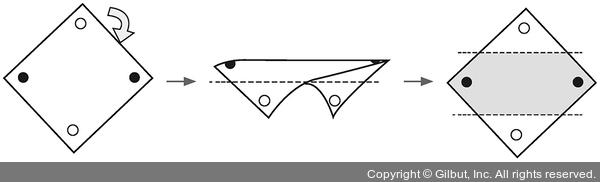
XOR 문제의 해결책은 종이를 휘어 주는 것이다. 즉, 좌표 평면 자체에 변화를 주는 것이다.
이를 위해 은닉층(hidden layer)을 만들어 공간을 왜곡하고 두 개의 퍼셉트론을 한 번에 계산할 수 있게 한다.
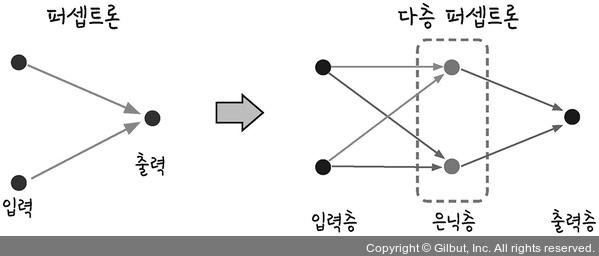
3-1 다층 퍼셉트론의 설계
다층 퍼셉트론이 입력층과 출력층 사이에 숨어있는 은닉층을 만드는 것을 그림으로 나타내면 아래와 같다.

가운데 숨어있는 은닉층으로 퍼셉트론이 각각 자신의 w와 b 값을 보낸다.
이 은닉칭에서 모인 값이 시그모이드 함수를 이용해 최종값(yout)으로 결과를 보낸다.
NAND 게이트와 OR 게이트, 이 두 가지를 내재한 각각의 퍼셉트론이 다중 레이어 안에서 각각 작동한다.
이 두 가지 값(n1, n2)에 대해 AND 게이트를 수행한 값이 yout이다.
4. 오차 역전파
신경망 내부의 가중치는 오차 역전파를 사용해 수정한다.
4-1. 오차 역전파의 개념
가중치와 바이어스를 실제로 구하기 위해 경사 하강법을 이용하면 된다. 임의의 가중치를 설정하고 결괏값을 이용해 오차를 구한다. 오차가 최소가 되는 점(미분했을 때 기울기가 0이 되는 지점)을 찾으면 된다.
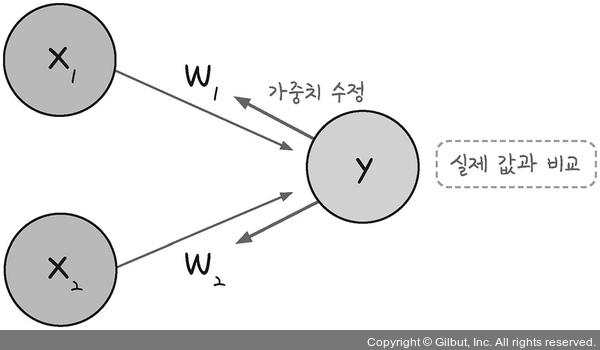

결괏값의 오차를 구해 하나 앞선 가중치를 차례로 거슬러 올라가며 조정해나간다. 최적화의 계산 방향이 출력층에서 시작해 앞으로 진행되므로 이를 오차 역전파(back propagation)이라 부른다.
- 임의의 초기 가중치를 준 뒤 결과(yout) 계산
- 계산 결과와 원하는 값 사이의 오차를 구함
- 경사 하강법을 이용해 바로 앞 가중치를 오차가 작아지는 방향으로 업데이트
- 오차가 더이상 줄어들지 않을 때까지 반복
→ 가중치에서 기울기를 뺐을 때 가중치의 변화가 없을 때까지 가중치 값 수정 반복.
5. 신경망에서 딥러닝으로

다층 퍼셉트론 + 오차 역전파 -> 신경망
신경망은 XOR 문제 가볍게 해결.. but 결과가 그렇게 좋지 않았다.
5-1 기울기 소실 문제와 활성화 함수
층이 늘어나면서 역전파를 통해 전달되는 가중치를 수정하기 위한 기울기의 값이 점점 작아져 맨 처음 층까지 전달되지 않는 기울기 소실(vanishing gradient) 문제가 발생했다. 활성화 함수로 사용된 시그모이드 함수의 미분값의 최대치가 0.3이기 때문이다. 이를 해결하기 위해 활성화 함수를 다른 함수로 대체하기 시작했다.
5-2 속도와 정확도 문제를 해결하는 고급 경사 하강법
- 확률적 경사 하강법
확률적 경사 하강법(Stochastic Gradient Descent, SGD)은 전체 데이터를 사용하는 것이 아니라, 랜덤하게 추출한 일부 데이터를 사용한다. 일부 데이터를 사용하므로 더 빨리, 더 자주 업데이트를 하는 것이 가능하다. 랜덤한 일부 데이터를 사용하기 때문에 중간 결과의 진폭이 크고 불안정해 보일 수도 있지만, 속도가 빠르면서도 최적 해에 근사한 값을 찾아내기 때문에 경사 하강법의 대안으로 사용되고 있다.
- 모멘텀
경사 하강법과 마찬가지로 매번 기울기를 구하지만, 이를 통해 오차를 수정하기 전 바로 앞 수정 값과 방향(+,-)을 참고하여 같은 방향으로 일정한 비율만 수정되게 하는 방법이다. 관성의 방향을 고려해 진동과 폭을 줄일 수 있다.
'Study > 딥러닝' 카테고리의 다른 글
| [모두의 딥러닝] 11장 데이터 다루기 (0) | 2021.05.29 |
|---|---|
| [모두의 딥러닝] 10장 모델 설계하기 (0) | 2021.04.17 |
| [모두의 딥러닝] 5장 로지스틱 회귀 (0) | 2021.04.11 |
| [모두의 딥러닝] 4장 오차 수정하기: 경사 하강법 (0) | 2021.04.10 |
| [모두의 딥러닝] 3장 가장 훌륭한 예측선 긋기: 선형 회귀 (0) | 2021.04.02 |




