| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 밑바닥부터 시작하는 딥러닝
- 베스트 모델
- 면접왕이형
- 보이스피싱
- 과적합
- 독서 #독서후기 #피로사회 #행동과잉 #긍정과잉
- GPT-3
- 뉴로 심볼릭
- 모두의 딥러닝
- 경제신문스크랩
- 안드로이드
- 딥페이크
- 밑시딥2
- 경사하강법
- 로지스틱 회귀법
- 코틀린
- 다중분류
- 선형회귀
- 예측선
- gradiant descent
- andoriod with kotlin
- MRC
- 안드로이드 구조
- 면접왕 이형
- ESG
- ESG 채권
- 학습 자동 중단
- 밑시딥
- k겹 교차검증
- nlp
- Today
- Total
Practice makes perfect!
[모두의 딥러닝] 4장 오차 수정하기: 경사 하강법 본문
1. 경사 하강법의 개요
3장에서 기울기 a에 따라 오차 값이 크거나 작아지는 것을 알았다.
기울기 a와 오차의 관계를 그리면 2차함수 그래프로 그릴 수 있는데, 이때 오차가 최소가 되는 값을 찾아야한다.
이때 미분 기울기를 이용해 오차가 가장 작은 방향으로 이동하는 것을 경사 하강법(Gradiant Descent)라 한다.
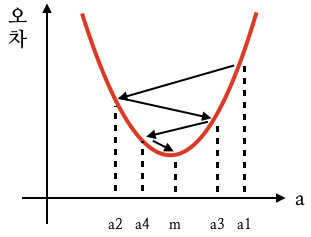
2차 함수에서 기울기가 0인(x축과 평행한) 점에서 최솟값을 갖는다. (위 그림에서 a=m일 때 최솟값을 갖는다)
즉 경사 하강법은 미분 값이 0인 지점을 찾는 것이다.
- 임의의 점 a1에서 미분하여 기울기 구함
- 구해진 기울기의 반대 방향으로 얼마간 이동시킨 a2에서 미분하여 기울기 구함
- 미분 값이 0이 될 때 까지 왔다갔다하며 반복
2. 학습률
2번 과정에서 적절한 이동 거리를 정해주기 위해 학습률(learning data) 이용한다.
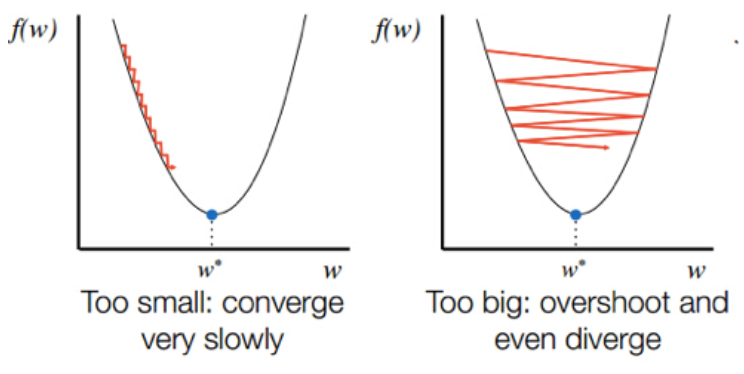
학습률이 너무 작으면 최솟값을 찾는데 너무 오랜 시간이 걸리고, 학습률이 너무 크면 값이 한 점으로 모이지 않고 위로 치솟아버린다.
3. 코딩으로 확인하는 경사 하강법
- 기울기와 오차의 관계를 2차 함수로 표현 (y절편 b와 오차의 관계도 이차함수로 표현됨)
- 적절한 학습률을 설정해 미분값이 0인 지점 찾기
- 최솟값 구하기
plt.figure(figsize=(8,5) # figure size 800x5000
plt.scatter(x,y) # 산포 그래프# 리스트로 되어 있는 x와 y값을 넘파이 배열로 바꿈
# (인덱스를 주어 하나씩 불러올 수 있게 함)
x_data = np.array(x)
y_data = np.array(y)
리스트도 인덱스가 있지만 몇 번째 데이터인가 정도만 의미하며 벡터, 행렬 계산이 불가능하다 -> 배열로 변경하여 계산한다
# 경사 하강법 시작
for i in range(2001):
y_pred = a * x_daya + b
error = y_daya - y_pred
# 오차 함수를 a로 미분한 값
a_diff = -(2/len(x_data))*sum(x_data*error)
b_diff = -(2/len(x_data))*sum(error)
# 학습률을 곱해 기존 값 업데이트
a = a - lr*a_diff
b = b - lr*b_diff
최소 제곱법 : x가 하나일 떄
경사 하강법 : x가 하나 이상일 때 (다중 선형 회귀)
4. 다중 선형 회귀란
정확한 예측을 하려면 추가 정보를 입력해야 하며, 정보를 추가해 새로운 값을 구하려면 변수의 개수를 늘려 다중 선형 회귀를 만들어야 한다.
공부한 시간 이외에 '과외 수업 횟수'라는 새로운 변수를 추가해보면 아래와 같다.
| 공부한 시간(x1) | 2 | 4 | 6 | 8 |
| 과외 수업 횟수(x2) | 0 | 4 | 2 | 3 |
| 성적(y) | 81 | 93 | 91 | 97 |
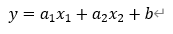
두개의 독립변수 x1과 x2가 생겼다.
하나의 독립변수일 때는 1차원이었던 예측 직선이 3차원 예측 평면으로 변했다. 따라서 좀 더 정밀한 예측을 할 수 있다.
'Study > 딥러닝' 카테고리의 다른 글
| [모두의 딥러닝] 10장 모델 설계하기 (0) | 2021.04.17 |
|---|---|
| [모두의 딥러닝] 6~9장 퍼셉트론, 다층 퍼셉트론, 오차 역전파 (0) | 2021.04.13 |
| [모두의 딥러닝] 5장 로지스틱 회귀 (0) | 2021.04.11 |
| [모두의 딥러닝] 3장 가장 훌륭한 예측선 긋기: 선형 회귀 (0) | 2021.04.02 |
| [모두의 딥러닝] 1장 나의 첫 딥러닝 (0) | 2021.03.26 |




